Esteu cercant informació sobre el hash a la criptografia? Si ho feu, heu arribat al lloc correcte.

En aquest article, explorarem més coses sobre el hash.

Hashing és una tècnica informàtica per identificar objectes o valors d’un grup d’objectes o valors.

Sona confús?

Intentem entendre amb l’exemple.

Bé, les universitats i les escoles proporcionen un número assignat de manera única a cadascun dels seus estudiants. Aquest número únic és el que identifica un estudiant i la informació relacionada amb ell. El mètode utilitzat per generar el número únic és Hashing.

Un altre exemple popular són les biblioteques on trobareu un munt de llibres a les prestatgeries. Cada llibre té el seu número d’identificació únic perquè pugui ubicar-se a l’enorme biblioteca!

Un exemple modern de hash serien els jugadors que es registren al joc. Valorant és un joc lliure de joc llançat per Riot. Ser lliure de joc significa que milions de persones jugaran el joc.

Cada jugador s’identifica mitjançant un valor d’identificació únic generat mitjançant un algorisme de resum.

A continuació, intentem entendre-ho amb més detall.

Què és Hashing?

Com s’ha indicat anteriorment, Hashing és el mètode per identificar un objecte d’un grup.

Cada objecte rep un número d’identificació únic un cop hash.

Però, què significa això tècnicament?

Tècnicament, una funció matemàtica genera una sortida de longitud fixa a partir de qualsevol cadena d’entrada de qualsevol longitud.

Les transaccions de Bitcoin es comparteixen quan les transaccions obtenen identificadors únics.

Si posa “Hola, món!” en un Algorisme de hash SHA-256, obtindreu la següent sortida:

Entrada: Hola món!

Sortida: dffd6021bb2bd5b0af676290809ec3a53191dd81c7f70a4b28688a362182986f

Aquí SHA256 genera la sortida a partir de l’entrada donada. Com podeu veure, hem utilitzat l’algoritme de hash de la funció Hash Secure (SHA-256). És un dels mètodes de hash més populars, incloent Message Direct (MD5) i Secure Hash Function (SHA1)..

Les propietats clau de la funció hash la fan fiable. Enumerem-los a continuació.

• Determinista → Això significa que la sortida serà la mateixa per a l’entrada donada en qualsevol circumstància.
• Resistent a la preimatge → La funció resistent a la preimatge garanteix que el valor de hash no sigui útil per generar el valor d’entrada.
• Computacionalment eficient → Les funcions de resum són eficients i no requereixen recursos computacionals enormes per executar-les.
• No es pot invertir enginyeria → La funció de hash no es pot invertir enginyeria.
• Resistent a les col·lisions → La resistència a la col·lisió garanteix que no hi hagi dues entrades que resultin en la mateixa sortida.

Aquí ja hem tractat Hashing criptogràfic per a principiants aquí. Mireu-ho aquí: Hashing criptogràfic: una guia per a principiants.

Però, si esteu aquí per obtenir coses avançades, no us decebrà.

Què és la funció Hash i les taules Hash? I com funcionen?

En aquesta secció, explorarem la funció de hash i les taules de hash amb més detall. En termes de hash, hi ha funcions de hash. Aquestes funcions s’encarreguen de convertir entrades grans en entrades fixes petites. Les taules de hash emmagatzemen les sortides.

En el procés de resum, els objectes es distribueixen en funció dels seus parells clau / valor a la matriu. Per tant, si passeu una matriu d’elements a les funcions de hash, obtindreu una sortida de matriu on cada un dels elements ara té una clau associada. El parell clau / valor és molt útil a l’hora d’accedir a elements en temps real, ja que ofereix un temps O (1) impressionant.

Per implementar funcions de hash, podeu treure els dos enfocaments preferits.

• El primer enfocament és utilitzar una funció hash per convertir un element en un enter. A continuació, es pot utilitzar la sortida sencera per accedir a l’element quan es posa a la taula de hash.
• Un altre pas és posar l’element a la taula de hash i després recuperar-lo mitjançant la clau hash.

En el segon mètode, les funcions seran les següents:

hash = hash_function (clau) índex = hash% array_size

Aquí, el hash i les mides de matriu són independents entre si. El valor de l’índex es calcula en funció de la mida de la matriu. L’operador de mòdul (%) ens permet calcular el valor.

En termes senzills, es pot definir una funció hash com una funció que pot assignar un conjunt de dades de mida arbitrària a un conjunt de dades de mida fixa. El conjunt de dades de mida fixa resultant es pot emmagatzemar a la taula de hash. Es donen molts noms als valors retornats per la funció hash. Es poden anomenar valors hash, hash, sumes hash i codis hash.

Escriure una bona funció Hash

Si voleu crear una bona funció o mecanisme de resum, heu d’entendre els requisits bàsics per crear-ne un. Enumerem-los a continuació:

• La funció hash ha de ser fàcil de calcular. Això vol dir que no caldrien molts recursos per executar-se.
• La funció hash ha de distribuir-se uniformement. En fer-ho, s’utilitzen les taules de hash per emmagatzemar els valors de hash de manera que no es produeixi l’agrupació.
• L’últim requisit és tenir menys o cap col·lisió. Cap col·lisió significa que no hi ha cap sortida única assignada a dues entrades.

Tècnicament, les col·lisions formen part d’una funció de hash i simplement no es poden eliminar d’una funció de hash. L’objectiu és crear una funció de resum que pugui oferir un bon rendiment de la taula de resum i resoldre les col·lisions mitjançant tècniques de resolució de col·lisions.

Per què necessitem una bona funció Hash?

Per entendre la necessitat d’una funció de resum útil, anem a l’exemple següent.

Suposem que volem crear una taula Hash mitjançant una tècnica de hash on les cadenes d’entrada seran les següents: {“agk”, “kag”, “gak”, “akg”, “kga”, “gka”}

Ara, creem una funció de hash que simplement afegeix el valor ASCII d’un (97), g (103) i k (107) i després fa un mòdul de la suma per 307.

És evident que la suma dels tres nombres també és 307. Això significa que si permutem tots els números i fem una operació de mòdul, obtindrem el mateix resultat. El resultat final seria emmagatzemar totes les cadenes al mateix número d’índex. El temps algorítmic per a la funció hash també seria complexitat O (n), cosa que no és desitjable. Podem concloure fàcilment que la funció de hash que hem descrit no és òptima per a escenaris de la vida real.

Per solucionar la funció hash, podem desplegar dividint la suma dels valors ASCII de cada element per un altre nombre primer, 727. En fer-ho, obtindrem una sortida diferent per a la nostra matriu de cadenes d’entrada donada..

Aprendre sobre les taules de hash

Les taules de hash són molt útils per emmagatzemar el resultat d’una funció de hash, que calcula l’índex i després emmagatzema un valor. El resultat final seria un procés computacional més ràpid amb complexitat O (1).

Les taules de hash són tradicionalment una bona opció per resoldre problemes que requereixen temps O (n).

Per tant, si agafeu una cadena de longitud fixa i proveu d’aprendre la freqüència de caràcters de la cadena.

Per tant, si string = “aacddce”, llavors un enfocament genèric és passar per la cadena diverses vegades i emmagatzemar cada freqüència.

# Proporciona una cadena d’entrada i compta la freqüència dels caràcters d’aquesta cadena

#L’algorisme és 0 (n) temps de complexitat

llista_temp = [] inici = "a" str = "ababcddefff" def alpha_zeta (): alpha = ‘a’ per a l’interval (0,26): temp_list.append (alpha) alpha = chr (ord (alpha) + 1) return temp_list temp_list = alpha_zeta () #print (temp_list) def caracter_freqüència (str, llista_temp): per a cadascun de temp_list: freq = 0 per a i a str: if (i == cadascun): freq = freq + 1 imprimir (cadascun, freq) caracter_freqüència (str, llista_temp)

La sortida del programa anterior serà la següent:

a 2 b 2 c 1 d 2 e 1 f 3 g 0 h 0 i 0 .. ..

Ara, implementem una taula de hash a C ++ i comptem la freqüència de caràcters.

#include use namespace std; int Freqüència [26]; int hashFunc (char c) {return (c – ‘a’); } void countFre (string S) {for (int i = 0; i< Longitud S. (); ++ i) {int index = hashFunc (S [i]); Freqüència [índex] ++; } Per a (int i = 0; i<26; ++ i) {cout << (char) (i + ‘a’) << ” << Freqüència [i]<< endl; }} Int main () {cout<<"Hola món"; countFre ("abbaccbdd"); }

La sortida del programa seria la següent:

a 2 b 3 c 2 d 2

La complexitat O (N) de l’algorisme el fa més ràpid en comparació amb altres enfocaments lineals.

Com es resolen les col·lisions

Hi ha maneres úniques de resoldre col·lisions en funcions de hash. Una de les formes més populars és l’encadenament separat, que també es coneix com a hash obert. S’implementa amb una llista enllaçada on cadascun dels elements de la cadena és una llista enllaçada. Aquest enfocament permet emmagatzemar elements i assegurar-se que certs elements només formen part de la llista enllaçada específica, resolent la col·lisió. Això significa que no hi ha dos valors d’entrada que puguin tenir el mateix valor de resum.

Explorant Hash a Python

En aquesta secció, veurem ràpidament el hash a Python. El motiu pel qual escollim Python és que és fàcil de llegir i pot ser utilitzat per tothom sense gaire problemes.

Com que el hash és una funció comuna, ja està implementat a la biblioteca Python. En utilitzar el mòdul, podeu proporcionar un objecte com a entrada i retornar el valor hash.

La sintaxi del mètode hash és:

hash (objecte)

Com podeu veure, inclou un únic paràmetre, que és l’objecte. L’objecte pot ser sencer, flotant o una cadena.

El valor retornat del mètode hash () depèn de l’entrada. Per a un enter, pot retornar el mateix nombre, mentre que per al decimal i la cadena serien diferents.

Vegem alguns exemples a continuació.

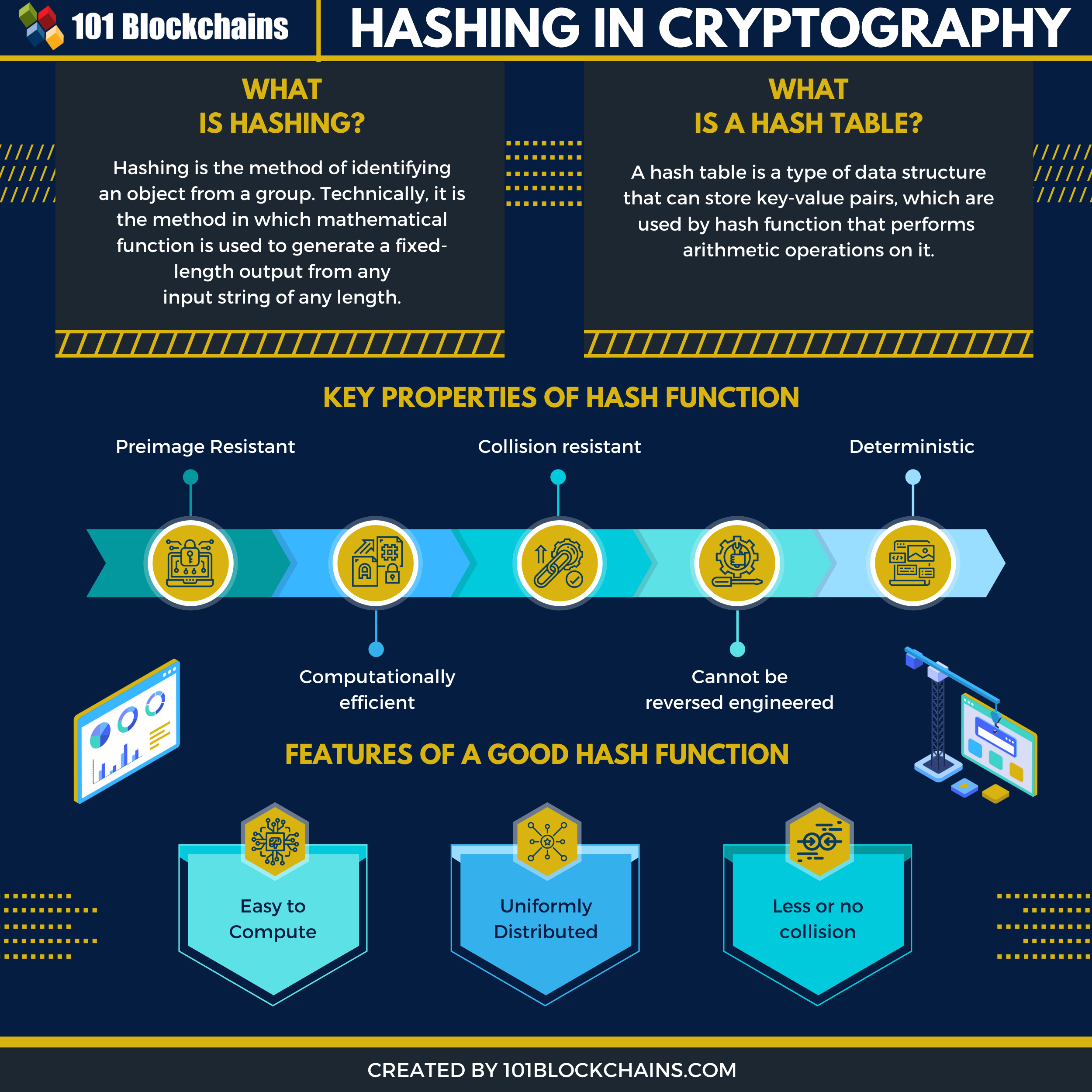
num = 10 deci = 1.23556 str1 = "Nitish" imprimir (hash (num)) imprimir (hash (deci)) imprimir (hash (str1))

La sortida del codi anterior és la següent:

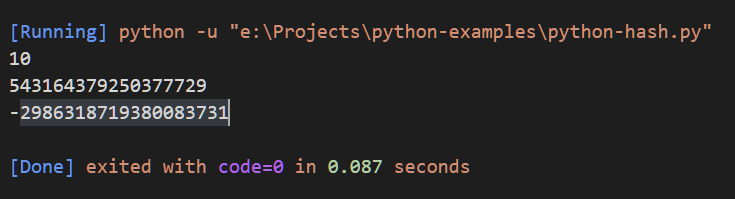
Tanmateix, el hash no es pot aplicar a tots els tipus d’objecte. Per exemple, si recordeu que vam crear una llista de la a a la z al nostre primer programa. Si intentem hash-lo, la finestra de sortida passarà per un TypeError: uneshable type: ‘list’

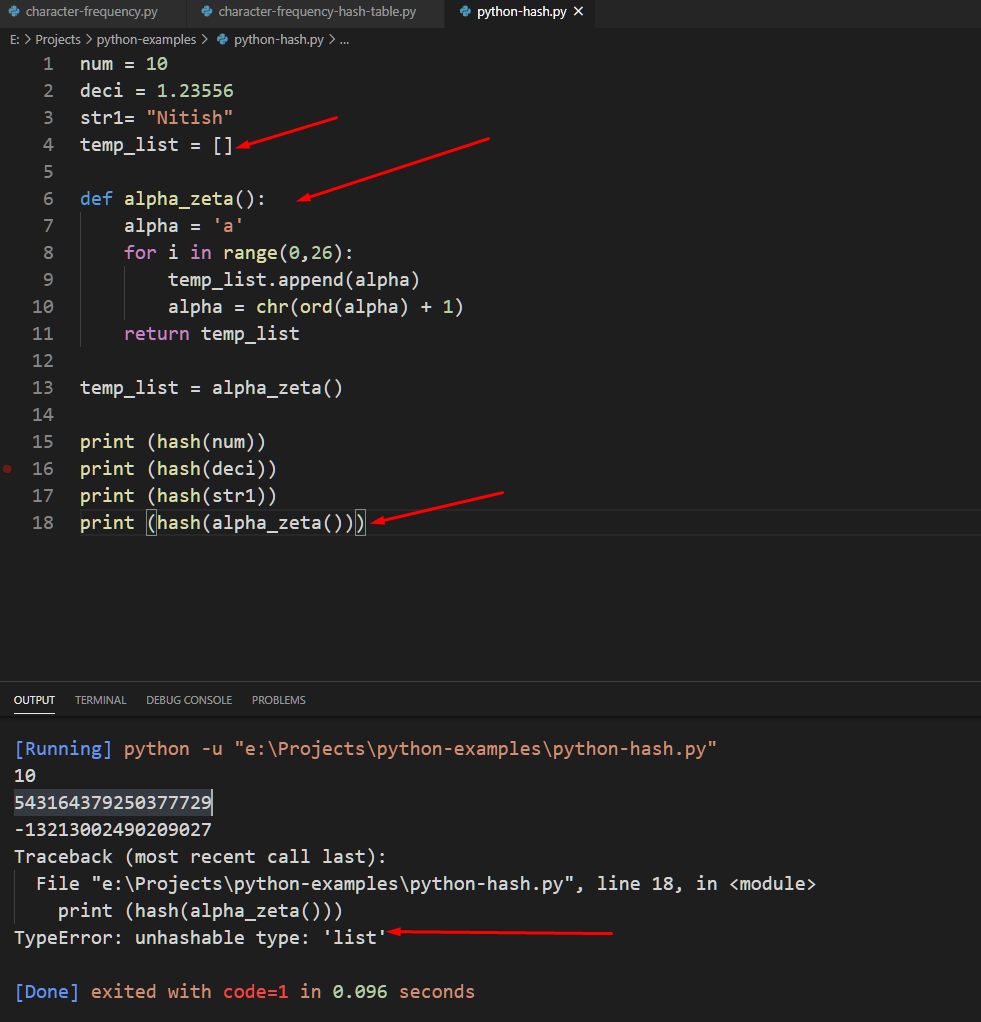
Per aplicar el hash a una llista d’objectes, heu d’utilitzar tupla.

vocals = (‘a’, ‘e’, ​​’i’, ‘o’, ‘u’) imprimir (hash (vocals)) Sortida ⇒ -5678652950122127926

Hashing a la criptografia

El hashing és útil per a la criptografia. Bitcoin utilitza hash per crear i gestionar arbres de Merkle

A més, el hashing ha estat part de la criptografia des de fa força temps. Tanmateix, el millor cas d’ús del hash és hash de contrasenyes i emmagatzemar-les.

Arbres Merkle

L’arbre de Merkle és una estructura de dades que és útil a l’hora de fer la verificació segura de dades en un gran conjunt de dades. Tant Bitcoin com Ethereum utilitzen arbres de Merkle per solucionar moltes barreres tecnològiques a l’hora d’emmagatzemar i accedir a dades en una xarxa oberta.

Qualsevol xarxa centralitzada no s’ha de preocupar d’emmagatzemar i accedir a les dades, ja que només hi ha una font tant per accedir com per emmagatzemar-les. Tanmateix, l’equació canvia quan hi ha una xarxa descentralitzada, ja que ara cal copiar les dades entre centenars de companys participants.

Els arbres de Merkle resolen el problema proporcionant una manera fiable i eficient de compartir i verificar dades entre companys.

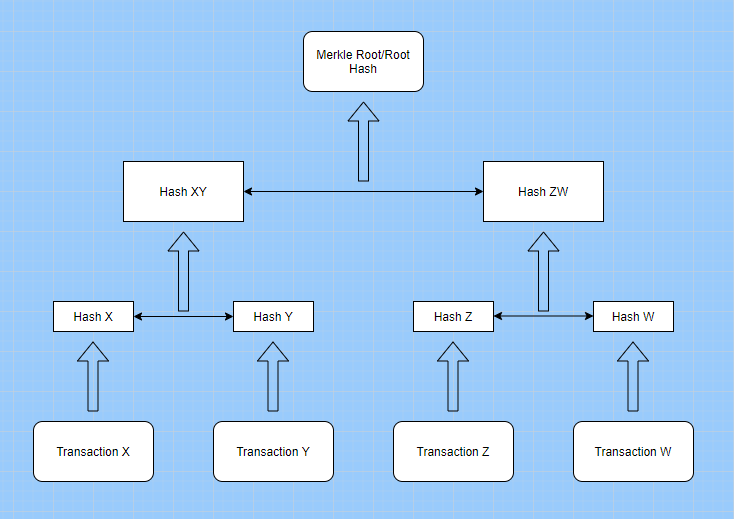
Exemple de Merkle Tree

Però, per què discutim aquí els arbres de Merkle? Els arbres de Merkle utilitzen el hash com a funcionalitat bàsica per connectar els diferents nodes i blocs de dades.

Merkle Trees és un arbre capgirat que pot resumir tot el conjunt de transaccions.

Si voleu obtenir més informació sobre els arbres de Merkle i sobre com utilitza el hash a la criptografia, consulteu la nostra guia detallada: Una guia dels arbres de Merkle. Allà, vam discutir com es fan els instruments dels arbres de Merkle en bitcoin i altres casos d’ús.

Procés de mineria

El procés de mineria també aprofita l’avantatge. Quan es tracta de mineria de bitcoins, s’afegeix un nou bloc a la cadena de blocs quan hi ha una demanda per a això.

Cal seguir un mètode per afegir el bloc a la cadena de blocs. Es genera un valor hash en funció del contingut del bloc quan arribi un bloc nou. A més, si el hash generat és més que dificultat de xarxa, s’inicia el procés d’afegir el bloc a blockchain.

Un cop fet, tots els companys de la xarxa reconeixen l’addició del nou bloc.

Però, rarament és així, ja que la dificultat de la xarxa, en la majoria dels casos, sempre és més alta en comparació amb el hash generat. Hi ha un altre aspecte que té un paper crucial en el procés de mineria. És el nonce.

El nonce s’afegeix al hash del bloc i és una cadena arbitrària. Un cop fet, la cadena concatenada es compara amb el nivell de dificultat. Si el nivell de dificultat és inferior a la cadena concatenada, es canvia el no fins que el nivell de dificultat sigui més alt.

El procés es pot resumir en els passos següents:

• El contingut es comparteix per crear un valor de hash cada vegada que es genera o pren un nou bloc,
• Es genera un nou valor de nonce i s’afegeix al hash
• El procés de hash té lloc a la nova cadena contactada
• A continuació, es compara el valor final del hash amb el nivell de dificultat de la xarxa
• si el valor final de hash és inferior al nonce, el procés es torna a repetir. El procés només s’atura quan el valor de hash és superior al no.
• El bloc s’uneix a la cadena un cop el nivell de dificultat és més alt
• Els miners assumeixen la responsabilitat de minar el nou bloc i compartir-ne els beneficis.

El terme “taxa de hash” també prové d’aquí. La taxa Hash és la velocitat a la qual tenen lloc les operacions de hash. Una taxa de hash més alta significa que els miners requeririen més potència de càlcul per participar en el procés de mineria.

Conclusió

Això ens porta al final de la nostra guia en profunditat de resum en criptografia. Hem tractat detalladament el hash i també hem explorat el codi que hi ha al darrere.

Què en penseu, doncs? Comenta a continuació i fes-nos-ho saber.

#FAQ

Què és el hash en la criptografia?

En criptografia, el hash és un mètode per convertir dades en una cadena única de text mitjançant un mètode eficient. A més, no hi ha limitacions en el tipus de dades ni en la seva mida; el hash funciona en totes.

Com s’utilitza el hash a la criptografia?

La criptografia utilitza el hash per hash de contrasenyes o generar números d’identificació únics.